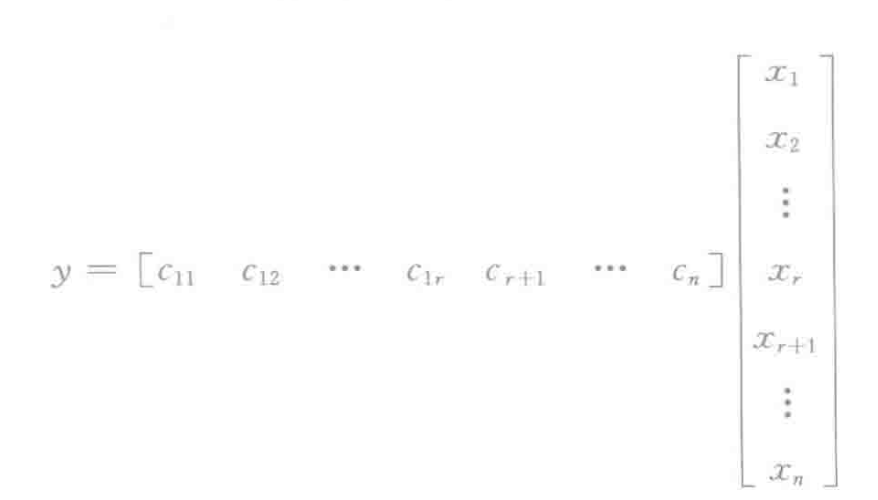2. 第二章
2.0 重点
2.1 基本概念
状态变量,状态向量,状态空间,状态方程,状态空间表达式的概念
非线性系统的状态空间描述
线性系统的状态空间描述
带t是时变的,不带t就是定常。
离散系统的状态空间描述
如果是线性的
写状态空间表达式的时候,写状态方程的时候: 微分放左边,没有微分的放右边
状态空间描述非唯一性:
这个要记住怎么用P变换的公式
最后这个公式很重要!记住,A是前逆后不逆,B是前逆,C是后不逆。
如何画状态变量图: 先画积分器,再画其他的。
例子:
2.2 传递函数与传递函数矩阵
单输入单输出系统
直接看结论
一些结论:
系统矩阵A的特征多项式就是传递函数的的分母多项式。
传递函数的极点就是矩阵A的特征值。
多项式 与 之和即为传递函数的分子多项式。
状态变量不同,同一系统的状态空间描述是不唯一的,但是传递函数是唯一的。
多输入多输出也是一样的
2.3 状态空间表达式的建立
2.3.1 从物理系统直接建立
2.3.2 从高阶微分方程建立
高阶微分方程的写法:
要注意,左边是没有的,是从开始,然后左边最高阶项系数一定是1。
然后右边是有的。
m<n时
当微分方程右边不含输入函数的导数的情况,即时:
这个直接记结论:
选取状态变量:
得到表达式:
输出方程:
所以此时的状态空间描述:
这个要记住!
当微分方程右边含输入函数的导数的情况,即时:
这里要引入算子符号来讨论,具体可以见p23
如果的时候
能控制标准型:
比如:
的能控标准型:重要‼️p24
能观标准型:
能观的A是能控的A的转置,能观的C是能控的B的转置,能观的B是能控的C的转置
m=n时
例子:
结果:
遇到这种题,一定要把a3, a2, a1, b3, b2, b1, b0都列出来!
2.3.3 由传递函数建立
g(s)要求是真分式,如果m=n,就要把常数项化出来。
只有当m=n的时候,才会有输入与输出间的直接传递项,一般情况都是严格真分式。
一般也是只讨论真分式。
直接分解
直接分解的推导过程我觉得要会。
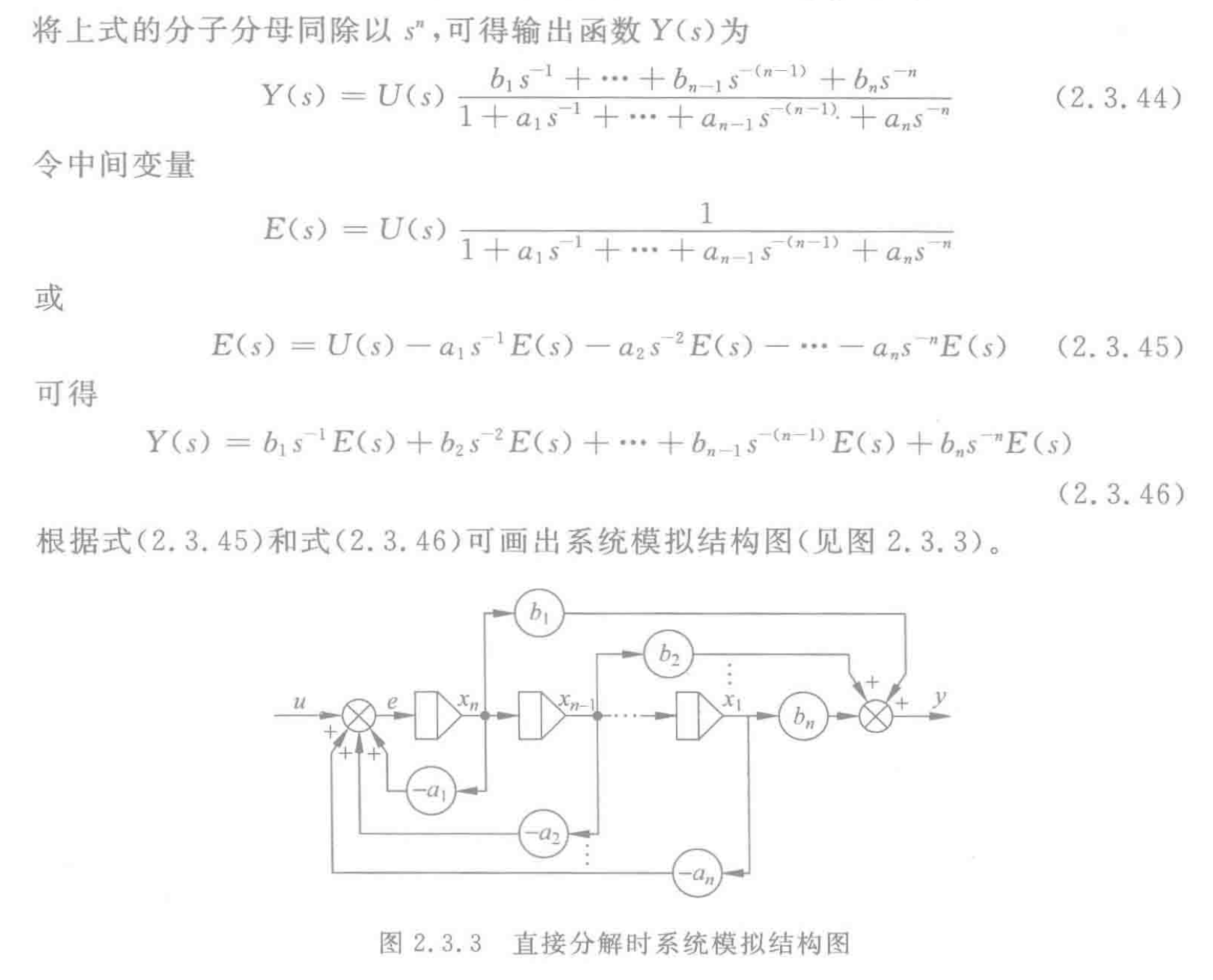
今选择各个积分器的输出作为系统的状态变量 , 于是状态空间表达式为:
要注意啊,现在这种表达式,公式25刚好分子比分母少一项,上面是b1-bn, 下面是a1-an要注意。
串联分解
要注意,上面刚好比下面少一维!
要记住两种表达式对应的画法!

这个分别对应两种画法!要记住!左边这个是 ,右边这个是 ,这个要记住。
状态变量就是每个积分器的输出。
结论直接记住!
并联分解
这个很好记,就是对角+若尔当型。
传递函数的极点互不相同的情况:对角形
注意:如何求c?
推导过程看看书p31
这个就是结论,直接记住,就是对角型。
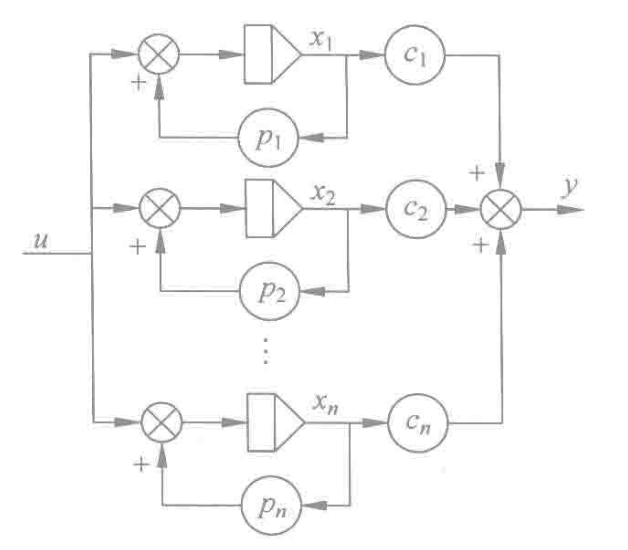
传递函数具有重极点的情况
就是若尔当+对角
注意,如何求c?
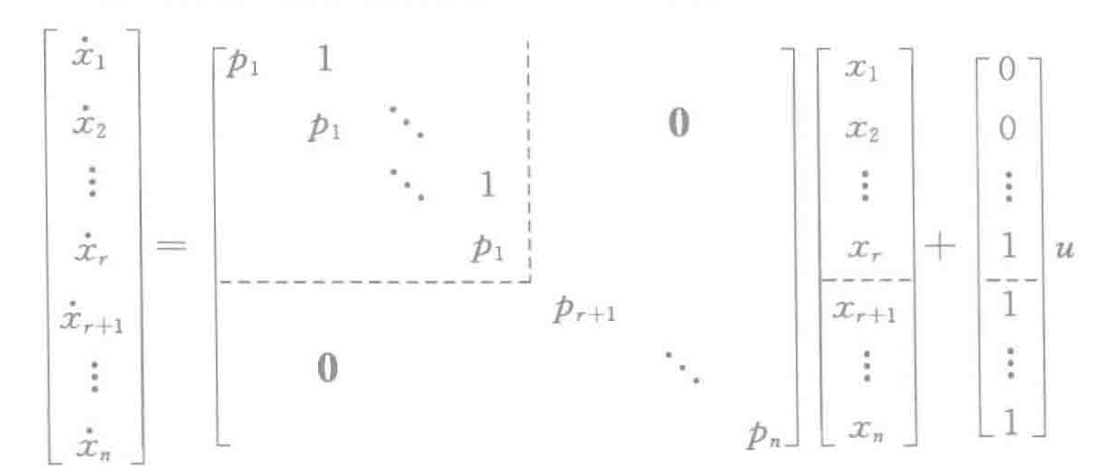
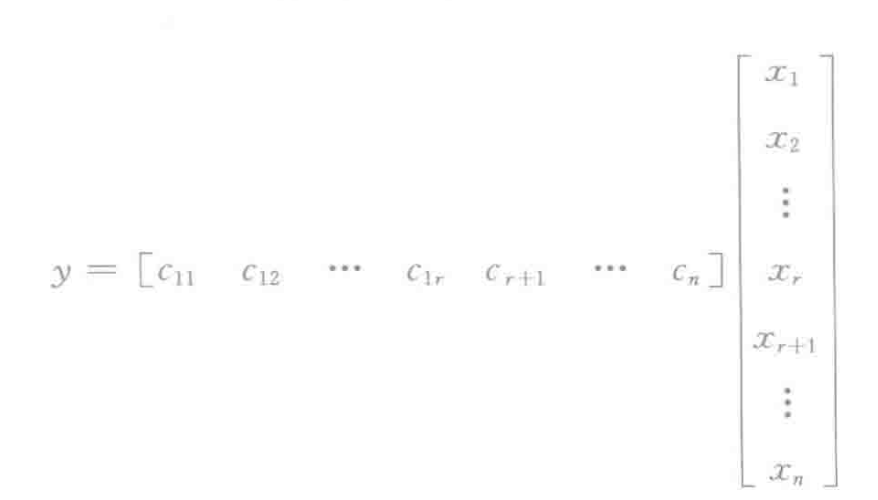
要记住,重根重了多少维,若尔当块就是几维的。
重要例题
这一部分求c的过程很重要!要记住,要复习!p34‼️
2.4 组合系统的状态空间表达式
多个系统的状态空间表达式和传递函数矩阵分别为:
2.4.1 并联
直接记结论:
状态空间:
传递函数:
2.4.2 串联
要满足要求,前一个的输出维度要等于后一个的输入维度,这个也很好理解,不然矩阵搞不到一起
状态空间:
传递函数:
2.4.3 反馈
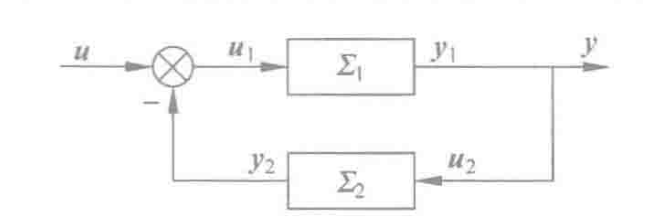
要求:
和 这个都是很好理解的。
动态反馈
直接记住结论:
状态方程:
传递函数:
要记住,很重要!注意1和2的顺序!
如果逆矩阵在前面,就是1在前面,如果逆矩阵在后面,就是2在前面。
常数反馈
要记住结论!
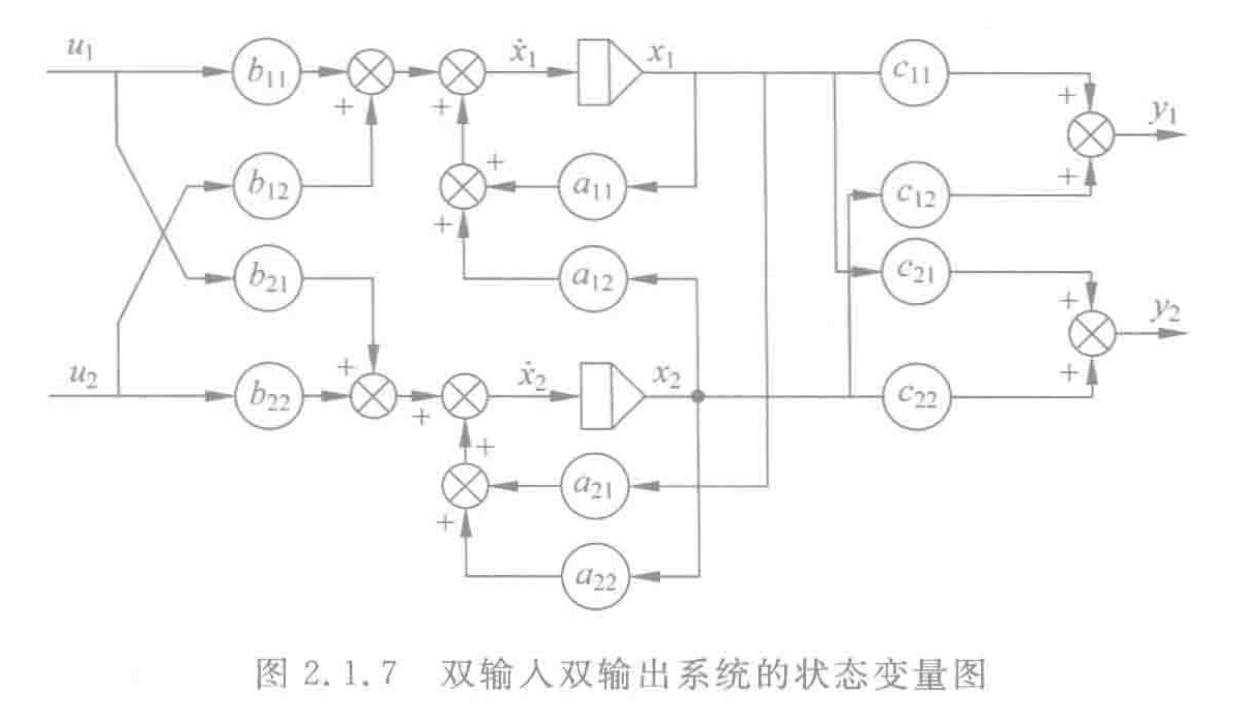
2.4.4 重要例题
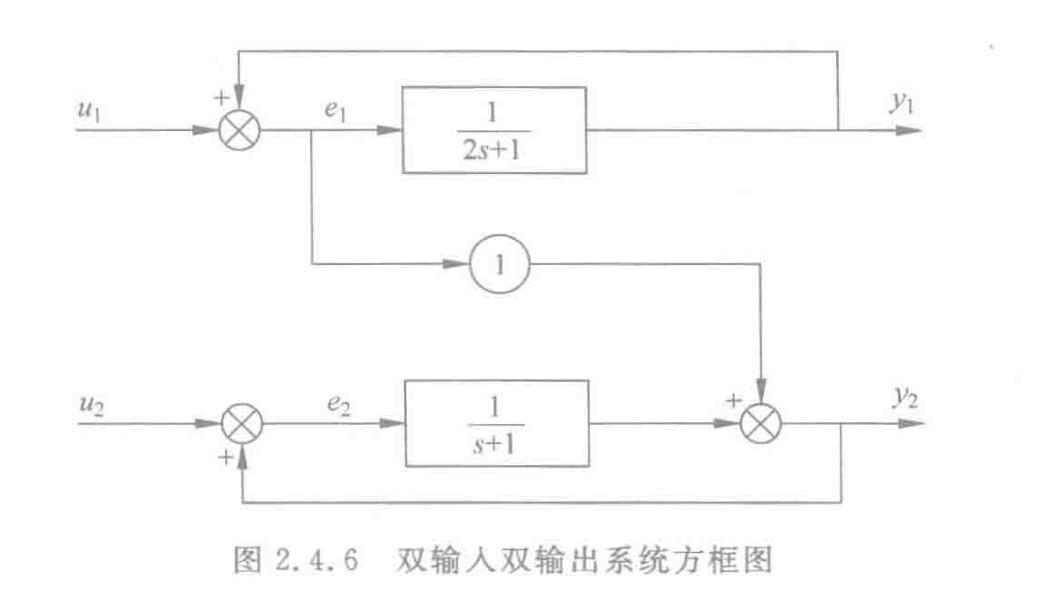
记住,误差函数e1,e2很重要,他就是矩阵A的构成!

2.5 线性变换
这一部分很重要,估计有计算题
2.5.2 化成对角型
这一部分比较熟悉了,求P即可,然后一定有n个特征值(互不相同),这个很熟了
就需要注意一个特殊情况。
如果矩阵A是友矩阵,可以直接得出P是Vandermonde矩阵。
比如p47的例题。
2.5.3 化成Jordan型
这一部分也是比较熟悉的,要注意:
有重根也有可能化成对角,p49
求广义特征向量的方法,p50‼️
2.5.4 特征值和传递函数矩阵的不变性
这个证明很简单。
原来是:
现在是:
带进去就能证明:
特征值的不变性也是一样,带进去就行了,很简单,p52.
2.6 离散事件系统的状态空间表达式
一样的
看看p55的例题。