4. 第四章

4. 第四章

4.1 定常离散系统的能控性

4.1.1 定义

离散系统的状态方程为：

\begin{matrix} (1) & x (k + 1) = A x (k) + B u (k) \end{matrix}

$\boldsymbol{u}(k), \boldsymbol{u}(k+1), \cdots, \boldsymbol{u}(N-1)$ $x(k)$ $x(N)=0$ 其中N事大于k的有限数，那么就称此系统在第k步上事能控的。如果对于每一个k，系统的所有状态都是能控的，则称系统是状态完全能控的，简称能控。

4.1.2 单输入离散系统能控性的判定条件

结论：

$\boldsymbol{x}(k+1)=\boldsymbol{A} \boldsymbol{x}(k)+\boldsymbol{b} u(k)$ $\left[\begin{array}{llll} \boldsymbol{b} \space \boldsymbol{A} \boldsymbol{b} & \cdots & \boldsymbol{A}^{n-1} \boldsymbol{b} \end{array}\right]$ $n$ 。

\begin{matrix} (2) & rank U_{c} = rank [\begin{array}{llll} b & A b & \dots & A^{n - 1} b \end{array}] = n \end{matrix}

这个经常用，要注意‼️（这个公式qbb老师在qq上给我讲解了🌍）

\begin{matrix} (3) & x (3) = A^{3} x (0) + A^{2} b u (0) + A b u (1) + b u (2) \end{matrix}

说明：n阶定常离散系统若在第n步上不能达到零状态，则永远不能转移到零状态。

4.1.3 多输入离散系统能控性的判定条件

判定方法和上面是一样的。

两个特点：

$\boldsymbol{U}_{\mathrm{c}}=\left[\begin{array}{llll} \boldsymbol{B} & \boldsymbol{A B} & \cdots & \boldsymbol{A}^{n-1} \boldsymbol{B} \end{array}\right]$ $n \times np$ 矩阵。根据判据，只要求它的秩等于n，所以在计算时不一定需要将能控性矩阵算完，发现已经满足n了，就可以停下来了。
为了把系统的某一处是状态转移到零状态，存在着许许多多的方式，因此可以在其中选择最优的控制方式。例如选择控制向量的范数最小。

4.2 定常连续系统的能控性

4.2.1 定义

\begin{matrix} (4) & \dot{x} = A x + B u \end{matrix}

$\boldsymbol{u}(t)$ $\left[t_{0}, t_{1}\right]$ $x\left(t_{0}\right)$ $x\left(t_{1}\right)$ $t_{0}$ $\boldsymbol{x}\left(t_{0}\right)$ 都是能控的, 就称此系统是状态完全能控的, 简称能控。

4.2.2 判断能控性

第一种方法：

\begin{matrix} (5) & \begin{matrix} U_{c} = [\begin{array}{llll} B & A B & \dots & A^{n - 1} B \end{array}] \\ rank [\begin{array}{llll} B & A B & \dots & A^{n - 1} B \end{array}] = n \end{matrix} \end{matrix}

$p=1$ $\operatorname{rank} \boldsymbol{U}_{\mathrm{c}}=\operatorname{rank}\left[\begin{array}{llll}\boldsymbol{b} & \boldsymbol{A} \boldsymbol{b} & \cdots & \boldsymbol{A}^{n-1} \boldsymbol{b}\end{array}\right]=n$ $\boldsymbol{U}_{\mathrm{c}}$ $n \times n$ $\boldsymbol{U}_{\mathrm{c}}$ 阵是非奇异（可逆）的。

第二种方法：

定理：如果线性定常系统：

\begin{matrix} (6) & \dot{x} = A x + B u \end{matrix}

的系统矩阵A具有互不相同的特征值，则系统状态能控的充分条件是，系统经线性非奇异变换后，A矩阵可以变换成对角阵。它的状态方程：

\begin{matrix} (7) & \begin{matrix} \dot{\hat{x}} = [\begin{array}{lll} λ_{1} & 0 \\ ⋱ \\ 0 & λ_{n} \end{array}] \hat{x} + \hat{B} u \end{matrix} \end{matrix}

$\hat{\boldsymbol{B}}$ 不包含元素全为0的行。

如果有重特征值，对应于每一个重特征值只有一个Jordan块，则系统状态完全能控的充要条件是，经线性非奇异变换后，系统化为若尔当标准型：

\begin{matrix} (8) & \begin{matrix} \dot{\hat{x}} = [\begin{array}{cccc} J_{1} & 0 & \dots & 0 \\ 0 & J_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & J_{k} \end{array}] \hat{x} + \hat{B} u \end{matrix} \end{matrix}

$\hat{\boldsymbol{B}}$ $\boldsymbol{J}_{i}(i=1,2, \cdots, k)$ 最后一行相对应的那些行, 其各行的元素不全为零。

特殊情况：

如果A为对角但是含有相同的元素（特征值相同但仍能对角化）情况下，或者不同若尔当块中有特征值相同的情况下，直接不能控。

4.2.3 线性定常连续系统的输出能控性

$\left[t_{0}, t_{1}\right]$ $\boldsymbol{u}(t)$ $\boldsymbol{y}\left(t_{0}\right)$ $\boldsymbol{y}\left(t_{1}\right)$ , 则称系统是输出完全能控的。

系统输出完全能控的充分必要条件是矩阵

\begin{matrix} (9) & [\begin{array}{lllll} C B & C A B & C A^{2} B & \dots & C A^{n - 1} B \end{array}] \end{matrix}

$q$ 。

注意两点：

状态能控性与输出能控性之间没有必然联系
上述判断输出能控性的准则同样适用于离散系统

4.3 定常系统的能观测性

能否通过对输出的测量来确定系统的状态变量，这个就是能观性问题。

4.3.1 定常离散系统的能观性

\begin{matrix} (10) & \begin{matrix} x (k + 1) = A x (k) + B u (k) \\ y (k) = C x (k) \end{matrix} \end{matrix}

$\boldsymbol{u}(k)$ $i$ $n-1$ $\boldsymbol{y}(i), \boldsymbol{y}(i+1), \cdots, \boldsymbol{y}(i+n-1)$ $i$ $x(i)$ $i$ $i$ 步上都是能观测的, 则称系统是状态完全能观测的, 简称能观测。

判据：

对于线性定常离散系统：

\begin{matrix} (11) & \begin{matrix} x (k + 1) = A x (k) + B u (k) \\ y (k) = C x (k) \end{matrix} \end{matrix}

状态完全能观测的充分必要条件是矩阵：

\begin{matrix} (12) & \begin{matrix} [\begin{matrix} C \\ C A \\ ⋮ \\ C A^{n - 1} \end{matrix}] \end{matrix} \end{matrix}

$n$ $nq \times n$ $U_o$ 表示。

4.3.2 定常连续系统的能观性

第一种方法：

\begin{matrix} (13) & \begin{matrix} [\begin{matrix} C \\ C A \\ ⋮ \\ C A^{n - 1} \end{matrix}] \end{matrix} \end{matrix}

的秩为n。

第二种方法：

$\boldsymbol{A}$ 有互不相同的特征值, 则系统状态能观测的充要条件是, 经线性等价变换把矩阵化成对角标准形后, 系统的状态空间表达式为：

\begin{matrix} (14) & \begin{matrix} \dot{\hat{x}} = [\begin{array}{llll} λ_{1} & 0 \\ λ_{2} \\ ⋱ \\ 0 & λ_{n} \end{array}] x \\ y = \hat{C} \hat{x} \end{matrix} \end{matrix}

$\hat{\boldsymbol{C}}$ 不包含元素全为零的列。

若尔当块的情况也是同理：

\begin{matrix} (15) & \begin{matrix} \dot{\hat{x}} = [\begin{array}{cccc} J_{1} & 0 \\ J_{2} \\ ⋱ \\ 0 & J_{k} \end{array}] \hat{x} \\ y = \hat{C} \hat{x} \end{matrix} \end{matrix}

$\boldsymbol{J}_{i}(i=1,2, \cdots, k)$ 第一列 $\hat{\boldsymbol{C}}$ 矩阵的所有各列, 其元素不全为零。

特殊情况：

与能控性情况相似，当矩阵A为对角形但含有相同元素时以及当矩阵A的若尔当标准形中有两个若尔当块的特征值相同，则上述两定理不适用。

4.5 能控性与能观性的对偶关系

$\Sigma_{1}$ 的状态空间方程为：

\begin{matrix} (16) & \begin{array}{l} \dot{x} = A x + B u \\ y = C x \end{array} \end{matrix}

$\Sigma_{2}$ 的状态空间表达式为：

\begin{matrix} (17) & \begin{array}{l} \dot{z} = A^{T} z + C^{T} v \\ w = B^{T} z \end{array} \end{matrix}

$\boldsymbol{x}$ $\boldsymbol{z}$ $n$ $\boldsymbol{u}$ $\boldsymbol{v}$ $p$ $q$ $\boldsymbol{y}$ $w$ $q$ $p$ 维。这两个系统称之为对偶系统。

此时：

$\Sigma_{1}$ $\Sigma_{2}$ $\Sigma_{1}$ $\Sigma_{2}$ 系统完全能控的充要条件相同。如方框图所示，重要方框图‼️

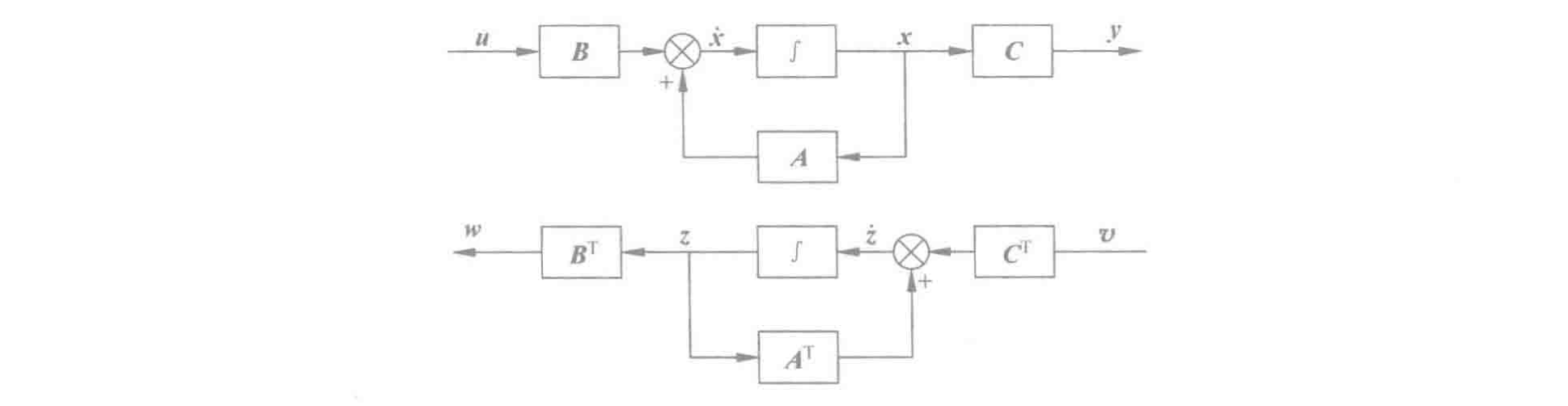
对偶原理：对偶系统的传递函数矩阵是互为转置的。

4.6 线性定常系统的结构分解

4.6.1 系统的能控性分解

\begin{matrix} (18) & \begin{matrix} {\begin{cases} \dot{x} = A x + B u \\ y = C x \end{cases} \end{matrix} \end{matrix}

如果一个系统的能控性矩阵rank < n。

$T_c$ $\boldsymbol{x}=T_{\mathrm{c}} \tilde{x}$ ，可使系统的状态空间表达式变换成以下形式：

\begin{matrix} (19) & \begin{matrix} {\begin{cases} \dot{\dot{x}} = \tilde{A} \tilde{x} + \tilde{B} u \\ y = \tilde{C} x \end{cases} \end{matrix} \end{matrix}

其中：

\begin{matrix} (20) & \begin{array}{l} \tilde{A} = T_{c}^{- 1} A T_{c} = [\begin{array}{cc} {\tilde{A}}_{11} & {\tilde{A}}_{12} \\ 0 & {\tilde{A}}_{22} \end{array}] \\ \tilde{B} = T_{c}^{- 1} B = [\begin{array}{c} {\tilde{B}}_{1} \\ 0 \end{array}] \\ \tilde{C} = C T_{c} = [\begin{array}{ll} {\tilde{C}}_{1} & {\tilde{C}}_{2} \end{array}] \end{array} \end{matrix}

这个变换的公式和第二章的是一样的，记住就行

$\widetilde{\boldsymbol{A}}_{11}$ 这部分能构成能控的。

‼️构造步骤：

$\boldsymbol{U}_{\mathrm{c}}=\left[\begin{array}{llll} \boldsymbol{B} & \boldsymbol{A} \boldsymbol{B} & \cdots & \boldsymbol{A}^{n-1} \boldsymbol{B} \end{array}\right]$ $n_{1}$ 个线性无关的列向量;
$\boldsymbol{T}_{\mathrm{c}}$ $n_{1}$ $\boldsymbol{T}_{\mathrm{c}}$ 为非奇异矩阵的条件下任意选择。

看看例题怎么选就行了：

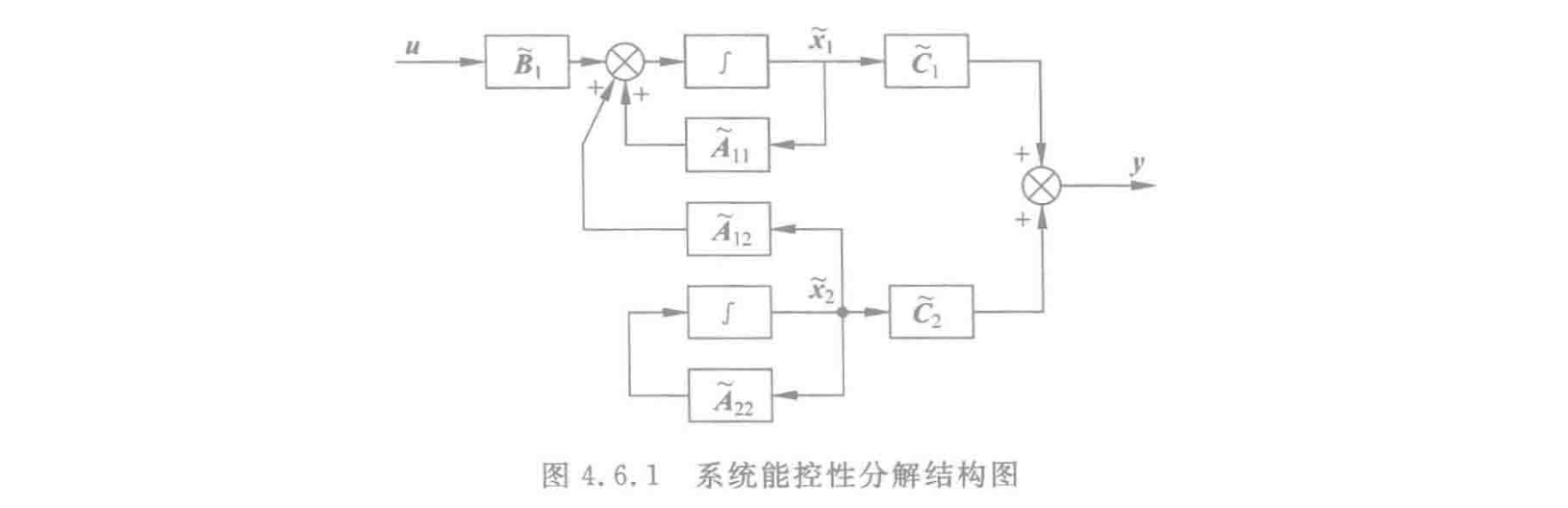
定理： 能控子系统的传递函数矩阵与原系统的传递函数矩阵相同，即：

\begin{matrix} (21) & {\tilde{G}}_{1} (s) = G (s) \end{matrix}

4.6.2 系统的能观性分解

定理：

$\boldsymbol{T}_{\mathrm{o}}$ $\boldsymbol{x}=\boldsymbol{T}_{\circ} \tilde{\boldsymbol{x}}$ 可使系统状态空间表达式变成：

\begin{matrix} (22) & \begin{matrix} {\begin{cases} \dot{\dot{x}} = \tilde{A} \tilde{x} + \tilde{B} u \\ y = \tilde{C} \tilde{x} \end{cases} \end{matrix} \end{matrix}

其中：

\begin{matrix} (23) & \begin{matrix} \tilde{A} = T_{o}^{- 1} A T_{0} = [\begin{array}{cc} {\tilde{A}}_{11} & 0 \\ {\tilde{A}}_{21} & {\tilde{A}}_{22} \end{array}] \\ \tilde{B} = T_{\circ}^{- 1} B = [\begin{array}{l} {\tilde{B}}_{1} \\ {\tilde{B}}_{2} \end{array}] \\ \tilde{C} = C T_{o} = [\begin{array}{ll} {\tilde{C}}_{1} & 0 \end{array}] \end{matrix} \end{matrix}

步骤：

$\boldsymbol{U}_{\mathrm{o}}=\left[\begin{array}{c} \boldsymbol{C} \\ \boldsymbol{C A} \\ \vdots \\ \boldsymbol{C A}^{n-1} \end{array}\right]$ $n_{2}$ 个线性无关的行向量。
$\boldsymbol{T}_{0}^{-1}$ $n_{2}$ $\boldsymbol{T}_{0}^{-1}$ 为非奇异矩阵的条件下任意选择。

能控是选列，这里是选行‼️

重要例题‼️

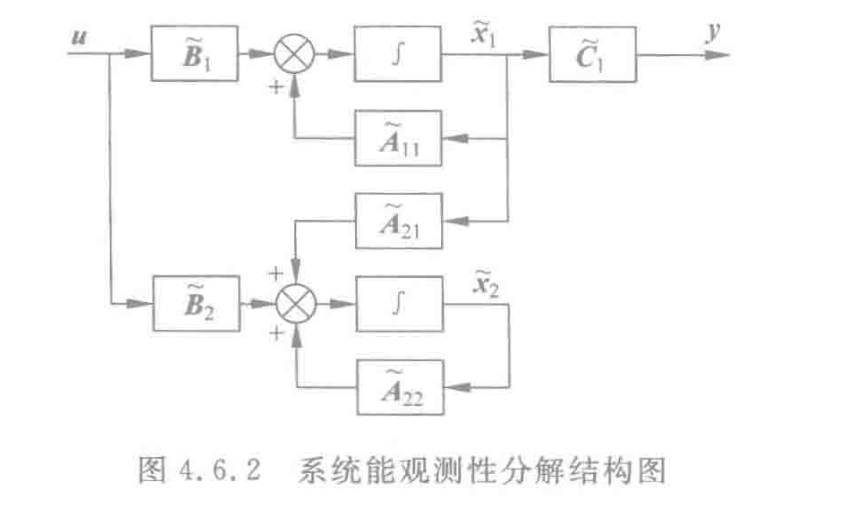
定理：

能观测子系统的传递函数矩阵与原系统的传递函数矩阵相同，即不能观测状态不会出现在系统传递函数矩阵当中。

4.6.3 系统按能控性与能观性进行标准分解

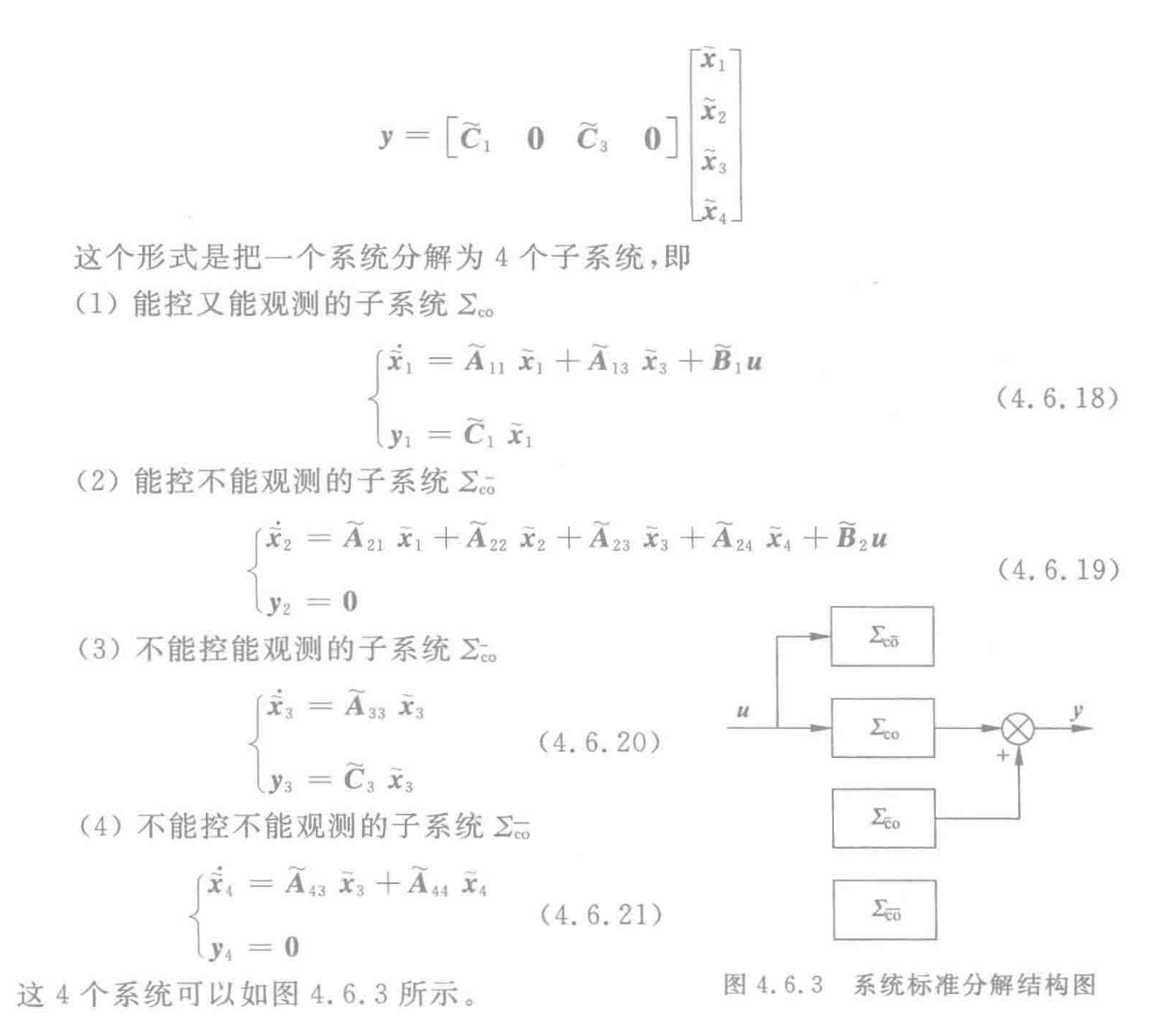
4.7 能控性、能观性与传递函数矩阵之间的关系

4.7.1 单输入单输出系统

系统的传递函数为：

\begin{matrix} (24) & g (s) = c (s I - A)^{- 1} b = c \frac{adj (s I - A)}{Δ (s)} b = \frac{N (s)}{D (s)} \end{matrix}

$N(s)$ $D(s)$ $\Delta(s)$ $\boldsymbol{A}$ $D(s)$ $N(s)=0$ $\Delta(s)=0$ $s$ $g(s)$ 的零点和极点。对此, 有如下定理。

定理‼️： $g(s)$ 中没有零点极点对消现象。

推论‼️：

一个系统的传递函数表示的是该系统既能控又能观的那一部分子系统
一个系统的传递函数若有零、极对消现象，则视状态变量的选择不同，系统或是不能控的或是不能观的。

4.7.2 多输入输出系统

系统传递函数为：

\begin{matrix} (25) & G (s) = \frac{C a d j (s I - A) B}{Δ (s)} \end{matrix}

$\Delta(s)=\operatorname{det}(s \boldsymbol{I}-\boldsymbol{A})$ $\boldsymbol{A}$ $\boldsymbol{G}(s)$ $m \times p$ 矩阵。对于此系统有如下结论。

结论：

$G(s)$ $\Delta(s)$ $\operatorname{Cadj}(s \boldsymbol{I}-\boldsymbol{A}) \boldsymbol{B}$ 之间没有非常数公因式, 则该系统是能控且能观测的。

此定理是多输入多输出系统能控能观测的充分条件而不是必要条件，它的充分性证明和前面定理相仿，不再多述。

4.8 能控标准型和能观标准型

4.8.1 系统的能控标准型

表示：

\begin{matrix} (26) & \begin{matrix} A = [\begin{array}{ccccc} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & \dots & 1 \\ - a_{n} & - a_{n - 1} & - a_{n - 2} & \dots & - a_{1} \end{array}], b = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 0 \\ 1 \end{matrix}] \end{matrix} \end{matrix}

如何转换成能控标准型：

存在非奇异变换：

\begin{matrix} (27) & \tilde{x} = P x 或 x = P^{- 1} \tilde{x} \end{matrix}

变换后：

\begin{matrix} (28) & \dot{\tilde{x}} = A_{c} \tilde{x} + b_{c} u \end{matrix}

$P$ 如何确定‼️？

直接上公式：

\begin{matrix} (29) & \begin{matrix} P = [\begin{matrix} p_{1} \\ p_{1} A \\ ⋮ \\ p_{1} A^{n - 1} \end{matrix}] \\ p_{1} = [\begin{array}{llllll} 0 & 0 & 0 & \dots & 0 & 1 \end{array}] {[\begin{array}{lllll} b & A b & A^{2} b & \dots & A^{n - 1} b \end{array}]}^{- 1} \end{matrix} \end{matrix}

4.8.2 系统的能观标准型

\begin{matrix} (30) & \begin{matrix} A = [\begin{array}{ccccc} 0 & 0 & \dots & 0 & - a_{n} \\ 1 & 0 & \dots & 0 & - a_{n - 1} \\ 0 & 1 & \dots & 0 & - a_{n - 2} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ 0 & 0 & \dots & 1 & - a_{1} \end{array}], c = [\begin{array}{lllll} 0 & 0 & \dots & 0 & 1 \end{array}] \end{matrix} \end{matrix}

变换矩阵T如何确定‼️？

\begin{matrix} (31) & \begin{array}{l} T = [\begin{array}{llll} T_{1} & A T & \dots & A_{1}^{n - 1} \\ T_{1} \end{array}] \\ T_{1} = {[\begin{array}{c} c \\ c A \\ ⋮ \\ c A^{n - 1} \end{array}]}^{- 1} [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix}] \end{array} \end{matrix}

4.9 系统的实现

给定传递函数矩阵，如何求出系统的状态空间表达式？

4.9.1 单输入单输出系统的实现问题

在此只讨论严格真分式传递函数的实现问题，即：

\begin{matrix} (32) & g (s) = \frac{β_{1} s^{n - 1} + β_{2} s^{n - 2} + \dots + β_{n - 1} s + β_{n}}{s^{n} + a_{1} s^{n - 1} + \dots + a_{n - 1} s + a_{n}} \end{matrix}

能控标准型实现：

\begin{matrix} (33) & \begin{array}{l} A = [\begin{array}{ccccc} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & \dots & 1 \\ - a_{n} & - a_{n - 1} & - a_{n - 2} & \dots & - a_{1} \end{array}], b = [\begin{array}{c} 0 \\ 0 \\ ⋮ \\ 0 \\ 1 \end{array}] \\ c = [\begin{array}{llll} β_{n} & β_{n - 1} & \dots & β_{1} \end{array}] \end{array} \end{matrix}

能观标准型实现：

\begin{matrix} (34) & \begin{aligned} A & = [\begin{array}{ccccc} 0 & 0 & \dots & 0 & - a_{n} \\ 1 & 0 & \dots & 0 & - a_{n - 1} \\ 0 & 1 & \dots & 0 & - a_{n - 2} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ 0 & 0 & \dots & 1 & - a_{1} \end{array}], b = [\begin{array}{c} β_{n} \\ β_{n - 1} \\ β_{n - 2} \\ ⋮ \\ β_{1} \end{array}] \\ c & = [\begin{array}{llllll} 0 & 0 & 0 & \dots & 0 & 1 \end{array}] \end{aligned} \end{matrix}

注意，并不能保证能控或者能观‼️

$g(s)$ $g(s)$ 的实现化为对角形或若尔当形，其电路模拟图为并联形式，构成并联实现，这在第2章中已介绍过。

4.9.2 多输入多输出系统的实现问题

行多时用能控，列多时用能观‼️‼️

4.9.3 传递函数矩阵的最小实现

$G(s)$ 的最小实现或不可约实现。它时最重要的实现，可以用最少数目的元件（积分器）来模拟系统。

$G(s)$ $A$ $B$ $C$ $D$ 的充要条件是系统状态完全能控且完全能观测的。‼️

如何构造最小实现？

传递函数矩阵的任何一种能控形或能观测形实现，再检查实现的能观测性或能控性，若已是能控能观测，则必是最小实现。
否则的话，采用结构分解定理，对系统进行能观测性或能控性的分解，找出既能控又能观测的子空间，从而得到最小实现。