5. 第五章
5.1 稳定性的基本概念
自治系统
零输入作用的系统,用如下方程描述:
其中,
受扰系统
本质:零输入响应
它是时间
平衡状态
在(1)描述的系统中,如果对于所有的
则称
当A非奇异,原点是系统唯一的平衡状态
当A奇异,则存在无穷多个平衡状态
欧几里德(Euclid)范数
即:n维空间中到平衡状态
稳定
对
的任一初始状态
则称
其实可以这样理解:
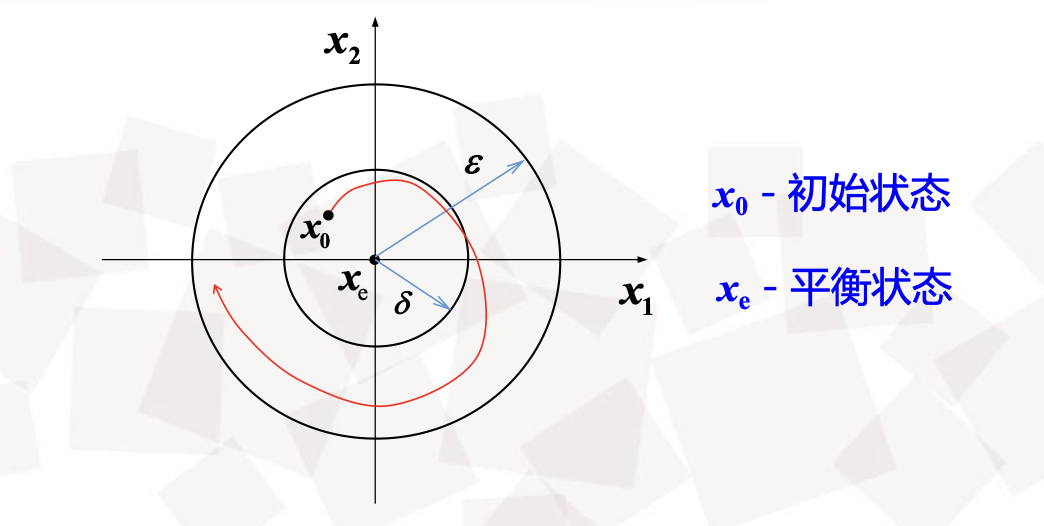
里面的小圆是
一般来说,小圆的大小是根据大圆大小和
一致稳定
如果
对于定常系统,稳定和一致稳定是等价的‼️。
通常要求系统是一致稳定的,以便在任意初始时刻
渐进稳定
如果
即:对于
则称平衡状态
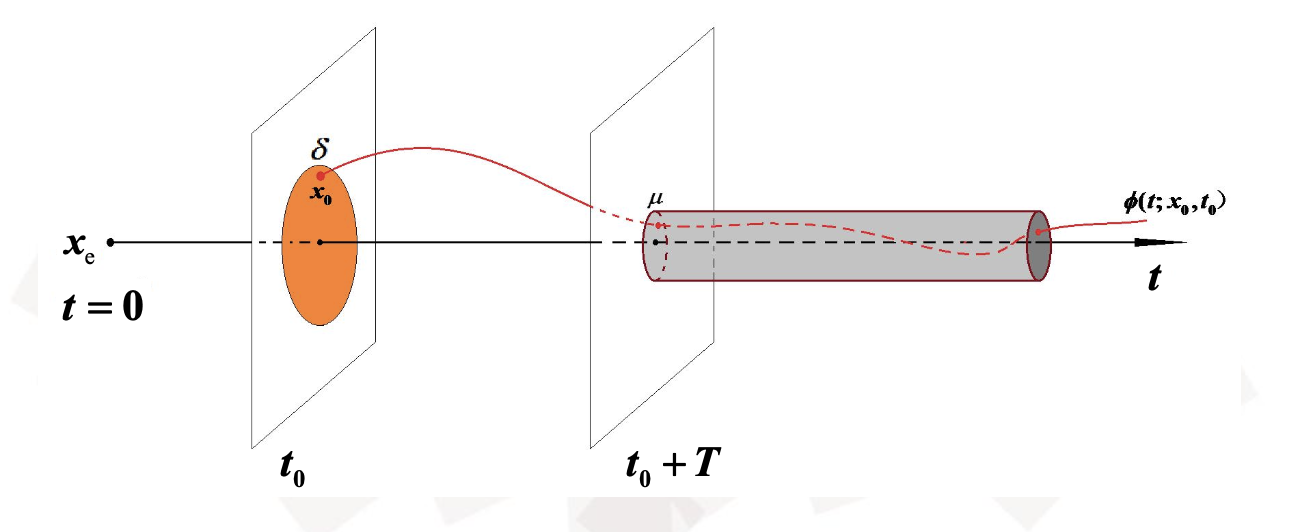
随着
既反映了运动的有界性,同时又反映了运动随时间变化过程的渐进性。
因此:渐进稳定=稳定+吸引
一致渐进稳定
如果实数
对于定常系统,渐进稳定和一致渐进稳定是等价的。
反正渐进的意思就是,和
大范围渐进稳定
如果从状态空间的任一有限非零初始状态
另一种说法: 如果
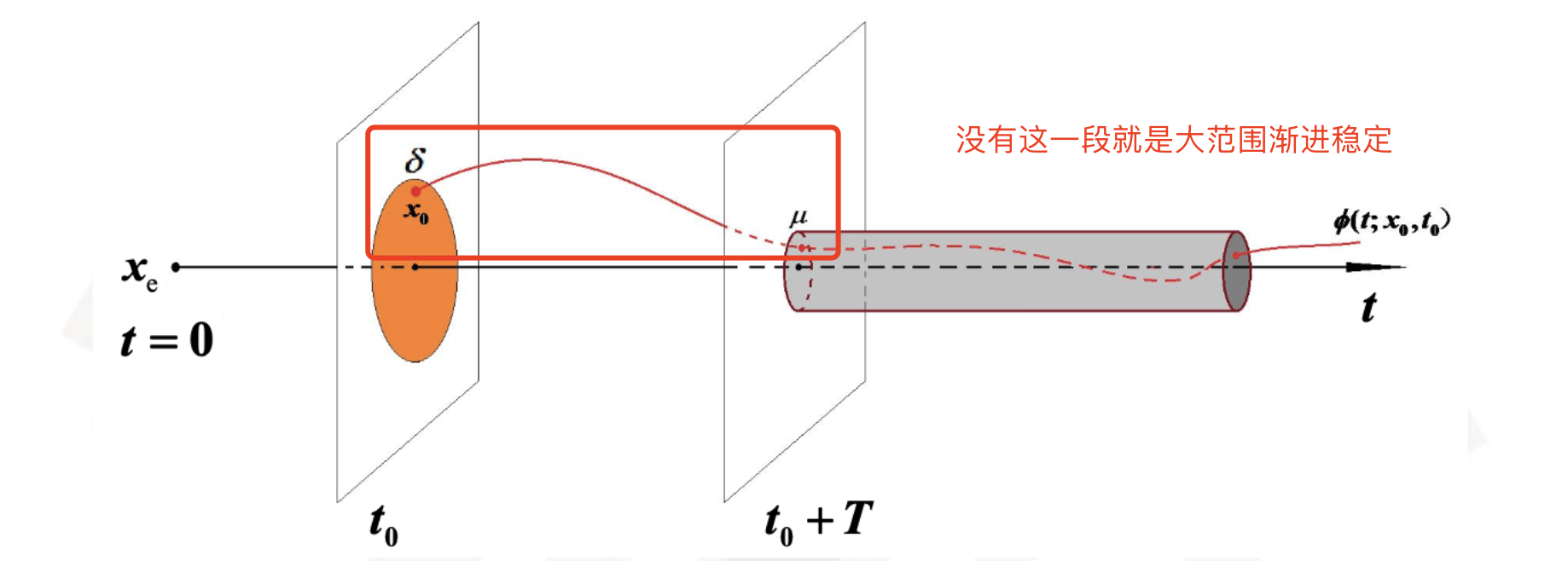
显然,大范围渐近稳定的必要条件是在整个状态空间中只有一个平衡状态。
对于线性系统,若其平衡状态为渐近稳定,则必然是大范围渐近稳定。
不言而喻,我们总是系统系统具有大范围渐进稳定性。
如果不是这样,我们就需要确定渐进稳定的引力域,而这项工作是困难的。
但是对于实际问题来说,确定一个足够大的渐进稳定范围,使得厨师扰动不超过它也就足够了。
不稳定
对于某个实数
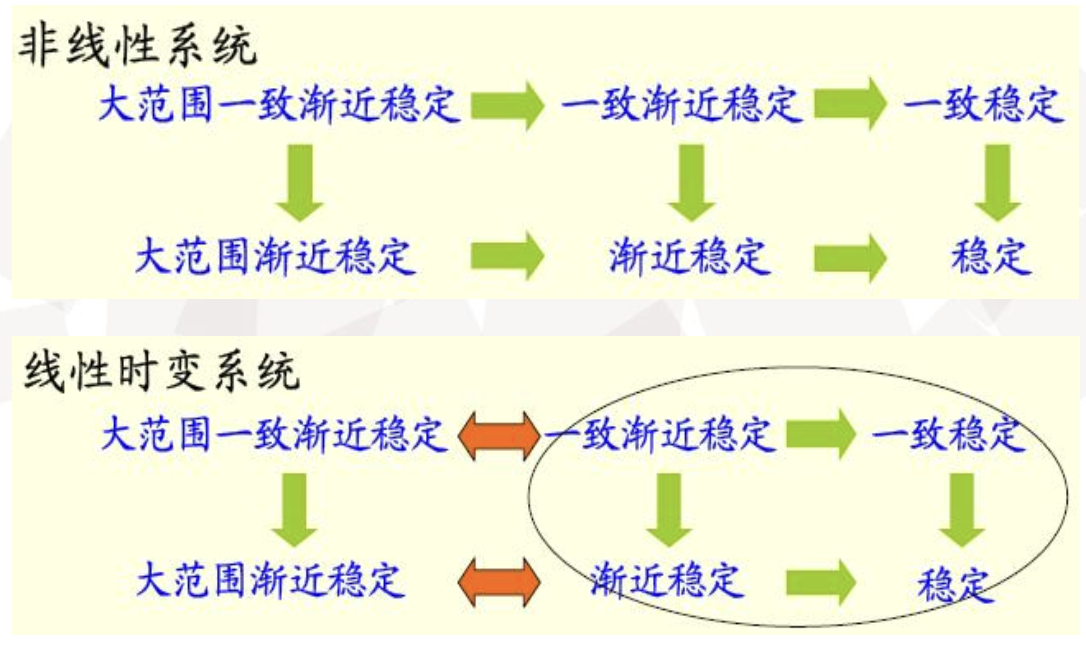
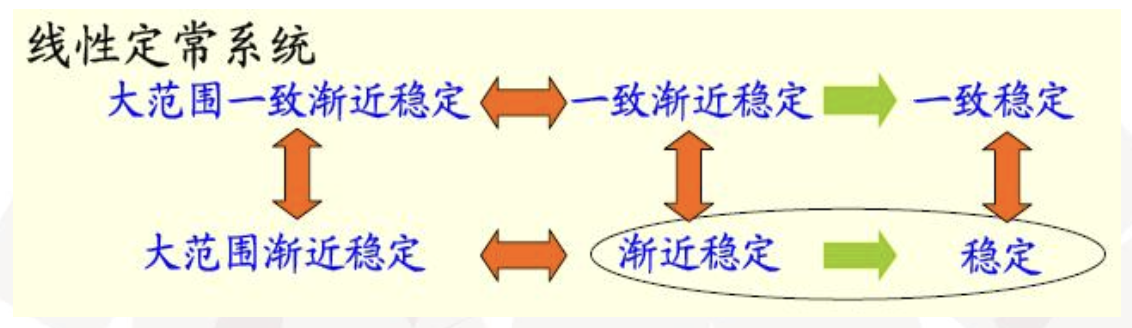
几种稳定性之间的关系‼️
正定函数
令
当
如果条件3中符号反向,则称
如果在
二次型
建立在李雅普诺夫第二方法上的稳定性分析中,有一类标量函数起着重要的作用,即为二次型函数:
P 为权矩阵,一般有:
常取
二次型一个重要结论(?)
对于二次型:
则
赛尔维斯特定理
当
如果
如果
一个易错概念
矩阵(半)负定当且仅当所有顺序主子行列式都是负的(非正的),这个是错的‼️
矩阵(半)负定当且仅当:
奇数阶顺序主子式为负(非正)
偶数阶顺序主子式为正(非负)
5.2 李雅普诺夫稳定性理论
5.2.1 李雅普诺夫第一方法
李雅普诺夫第一方法又称为间接法,其基本思想是解出系统的状态方程,然后根据状态方程解的性质判别系统的稳定性。
对于线性系统,只须求出系数矩阵的特征值即可判断其稳定性。
对于非线性系统,则可以通过线性化处理,得到一次近似的线性化方程,然后再来判断
若系统存在一个以上的平衡状态,则要对每个平衡状态进行研究。
显然,对于线性系统,只需要求出系数矩阵的特征值就能判断其稳定性。
考察非线性系统,设在零输入下状态方程为:
讨论系统在其平衡状态
引入新的向量
从而得到一次近似的线性化方程:
其中
出现在雅可比矩阵
结论‼️:
如果
如果
如果
重要例题:

5.2.2 李雅普诺夫第二方法
能量函数的概念:
李雅普诺夫稳定性理论建立了系统能量与稳定性之间的关系。
如果系统有一个渐近稳定的平衡状态,则当它转移到该平衡状态的邻域内时,系统所具有的能量随着时间的增加而逐渐减少,直到在平衡状态达到最小值。需要有一个抽象的能量函数来描述系统的虚拟能量。
能量函数:状态和时间的标量函数
此能量函数称为李雅普诺夫函数,记作
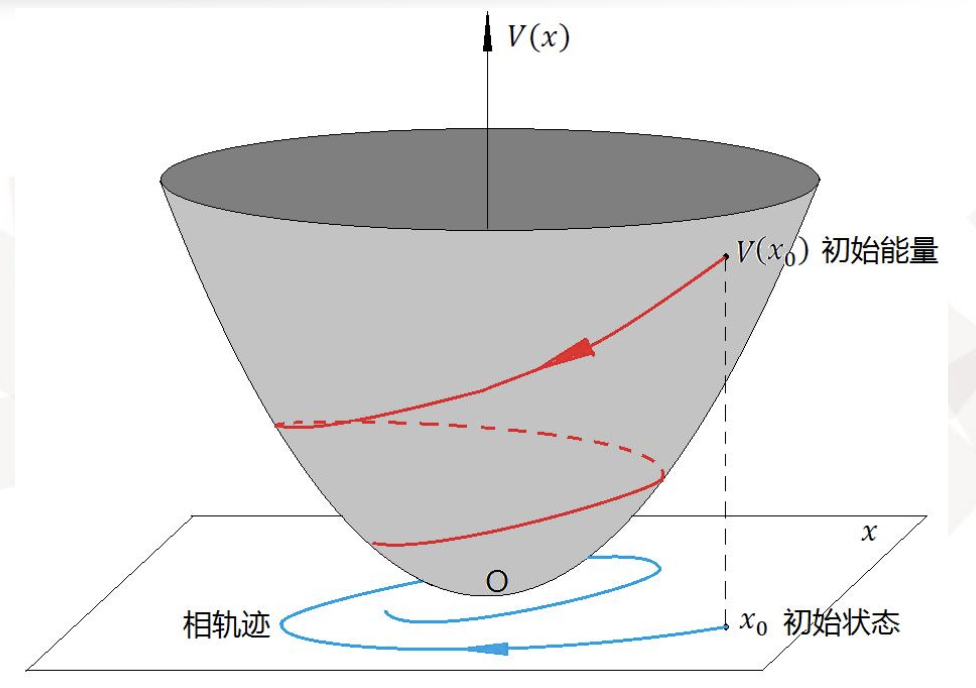
通过分析系统能量的变化来确定系统运动的稳定性对一个给定的系统,如果能够找到一个正定的标量函数,它沿着轨迹对时间的导数总是负值,则随着时间的增加,
定理:
假设系统的状态方程为:
如果存在一个具有连续偏导数的标量函数(李雅普诺夫函数)
那么系统在原点处的平衡状态时一致渐进稳定的。如果随着
比如:

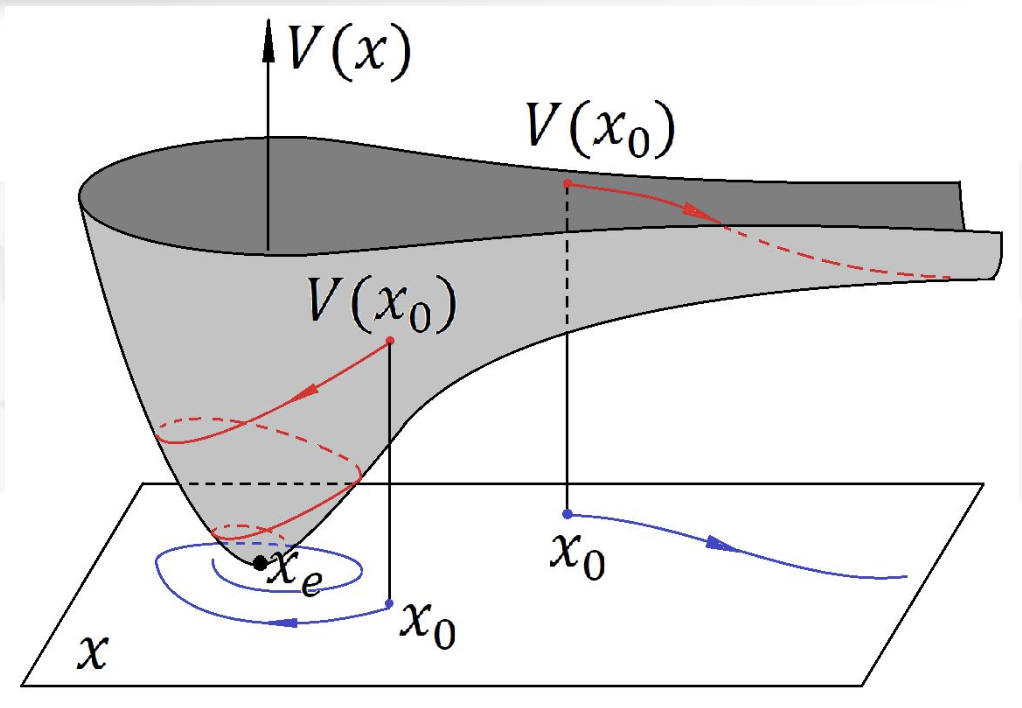
注意:如果只能找到
也就是第二个条件还不够符合,则只能得出稳定的结论,不能得出渐进稳定的结论。
这个时候运动轨迹将落在某个特定的曲面上,而不会收敛于原点,属于临界稳定。
比如:

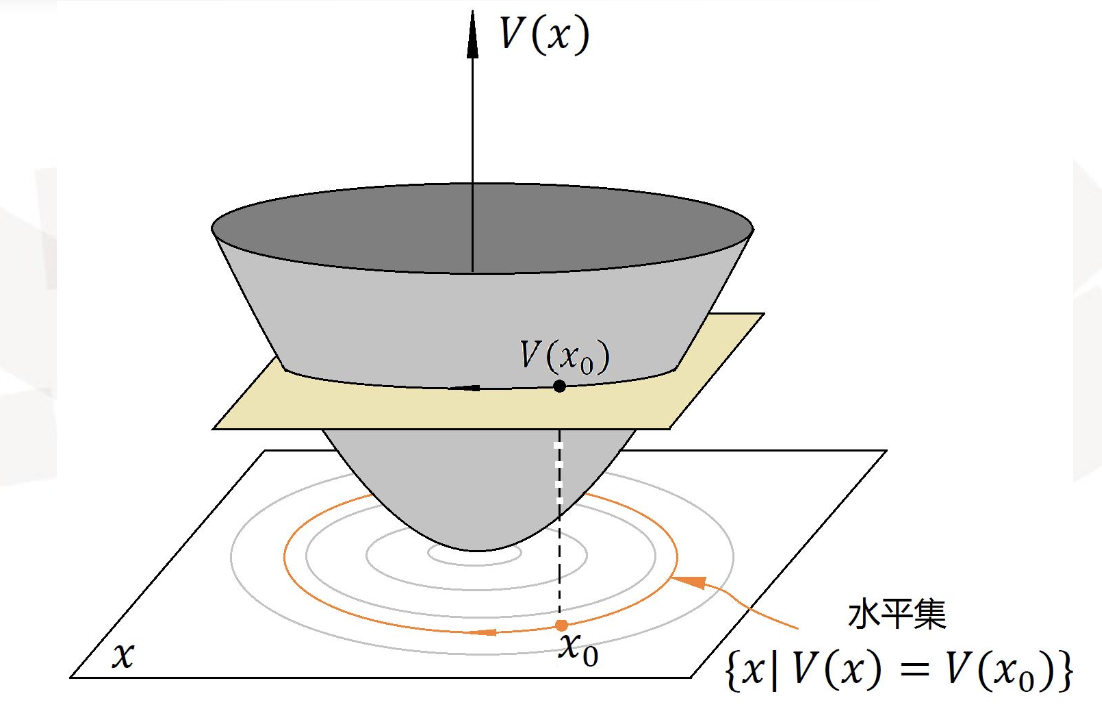
补充定理:
对于系统:
如果存在一个标量函数
在

定理:
对于系统:
如果存在一个标量函数
则系统在原点处的平衡状态时一致稳定的。
需要注意:
如果系统的平衡状态
定理:
对于系统:
如果存在一个标量函数
则系统在原点出的平衡状态是不稳定的。
比如:

5.2.3 一些说明
对于一个给定的系统,李雅普诺夫函数不是唯一的。
对于非线性系统能给出关于在大范围内稳定性的信息。
若系统稳定,则一定存在满足条件的李雅普诺夫函数,但是从特定李雅普诺夫函数得到的稳定性条件是充分的而不是必要的。
因此,若没能找到合适的李雅普诺夫函数就不能得出该系统稳定性方面的任何结论。
李雅普诺夫函数只能判断其定义域内平衡状态的稳定性。
如果系统的原点是稳定的或渐近稳定的,那么具有所要求性质的李雅普诺夫函数一定是存在的。经验表明,李雅普诺夫函数最简单的形式是二次型,即
5.3 李雅普诺夫方法在线性系统中的应用
利用李雅普诺夫方法判断线性系统的稳定性
连续系统
定理:
问题其实就是如何通过
设系统的状态方程为:
此时的标量函数
注意:
如果
如果取一个任意的正定矩阵(或者,若
为了确定
只要矩阵
重要例题:

离散系统
直接看公式就行了:
是正定的就行了。